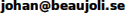
Voilà comment ordonner le Rubik's Cube que vous avez en main:1. Choisissez les six couleurs de base. En appuyant sur la case centrale de l'une des faces du modèle en 2D, vous pouvez changer la couleur de base de toute cette face. Faites de telle sorte que les couleurs des six cases centrales soient bien placées, l'une par rapport aux autres, quand vous comparez avec votre propre cube. 2. Replacez les autres cases colorées du cube de départ en 2D en appuyant sur toutes les cases mal placées, afin de les noircir. Ensuite appuyez sur l'une des étiquettes apparues à côté du modèle afin d'en selectionner la couleur puis appuyez sur les bonnes cases pour les colorer. |
3. À tout moment, vous pouvez comparer votre propre cube avec les modèles en 2 ou 3D. Vous pouvez faire tourner le modèle en 3D (soit le cube entier, soit l'une de ses faces) en appuyant et tirant dans les directions naturelles. Quand le cube de départ sur l'écran a la même apparence que votre propre cube et si vous êtes satisfait avec le but proposé, vous pouvez appuyer sur le bouton avec la flèche et le point d'interrogation pour démarrer le calcul automatique d'une solution. Celle-ci apparait sur le tableau blanc à gauche. Douze symboles différents indiquent les douze rotations élémentaires possibles. (Chaque rotation élémentaire correspond à un quart de tour de l'une des faces dans un sens ou l'autre. Les cases centrales des différentes faces ne changent jamais de place.) Ces symboles sont les mêmes que ceux sur les bouttons en dessous des cubes. Si vous voulez, vous pouvez donc tester l'effet du boutton sur le cube avant d'effectuer la rotation élémentaire sur votre propre cube. À la longue vous risquez cependant de trouver cette méthode fastidieuse. Pour comprendre plus rapidement la signification des symboles, vous pouvez penser de la façon suivante: La face qui se trouve au milieu du croisement du modèle en 2D correspond à la face de dessus de votre cube physique. Celle juste en dessous du croisement correspond à la face physique tournée vers vous. La face tout en haut du modèle en 2D correspond donc à la face physique tournée vers l'écran de votre ordinateur. Pour comprendre les symboles des rotations élémentaires, pensez maintenant qu'ils montrent le cube vu d'en haut. Les symboles contenant des flèches en ligne droite sont relativement simples à interpréter si l'on pense au fait qu'une telle flèche est tracée le long de l'un des bords de la face supérieure. Les quatre autres symboles (avec des flèches courbées) indiquent des rotations de la face de dessus ou de celle de dessous. Une grande flèche courbe autour d'un carré plus petit indique une rotation de la face de dessus. Une petite flèche courbe à l'interieur d'un carré plus grand indique une rotation de la face de dessous. (Si le cube était en verre, de telle sorte qu'on puisse voir à travers, le carré représenterait les contours de la face supérieure tandis que la petite flèche serait gravée sur la surface inférieure et pour cette raison semblerait plus petite puisqu'éloignée de quelques centimètres de plus quand on regarde d'en haut!)
Le programme aurait pu être écrit de manière à toujours calculer le chemin le plus rapide (minimant le nombre de rotations élémentaires) du départ au but. Hélas l'utilisateur aurait souvent du attendre la réponse quelques annés. Alors au lieu de cela, le programme utilise une méthode plus humaine avec un nombre de buts intermédiaires avant d'atteindre le but final. Parfois on peut remarquer que le programme indique une rotation élémentaire puis immédiatement après le mouvement opposé qui annule l'effet du précédent. Bien sûr, cela semble tout-à-fait inutile mais peut se produire dans le cas où le programme choisit un certain mouvement comme le dernier anneau d'une chaine pour atteindre un but intermédiaire puis juste ensuite le mouvement opposé comme premier anneau de la chaine qui mène au prochain but.
Le programme est écrit par Johan Dufour.
Bienvenue à envoyer vos commentaires à: 
Le modèle en 3D du cube est très inspiré par l'applet de Karl Hörnell, "Rubik Unbound". (Vous trouverez plus d'applets intéressants sur sa page: www.javaonthebrain.com)